光的干涉

• 杨氏双缝干涉
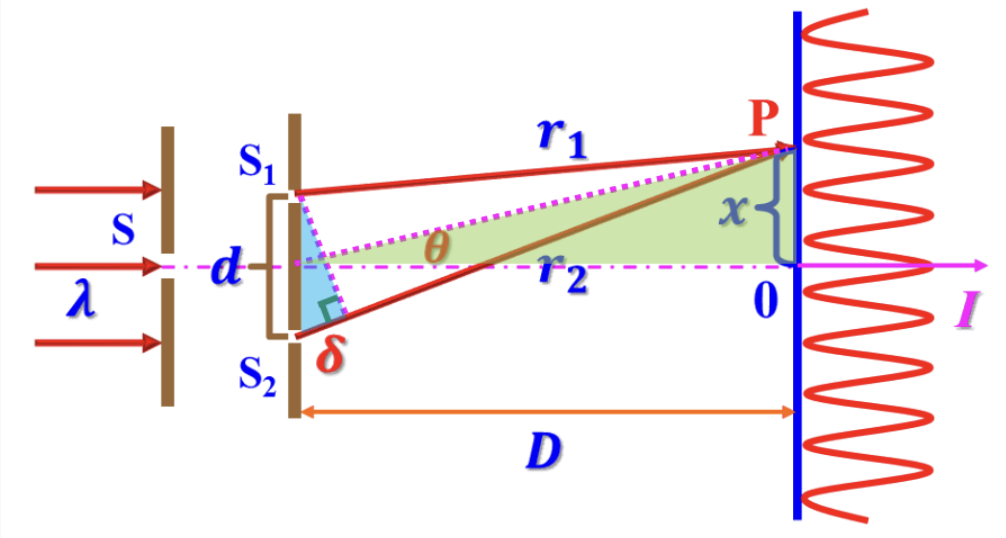
  • 原理图
    • 
  • 光程差分布
    • 亮纹中心： $\delta=\pm k\lambda,k\in \mathrm N^*$
    • 暗纹中心： $\delta=\pm\frac{2k-1}{2}\lambda,k\in \mathrm N^*$
    • 光程差相同的点构成同一条干涉条纹。
    • 相邻两条亮纹或暗纹之间的光程差的变化为 $\lambda$ 。
  • 位置分布
    • 亮纹中心： $x=\pm k\frac{D}{d}\lambda,k\in\mathrm N^*$
    • 暗纹中心： $x=\pm \frac{2k-1}{2}\frac{D}{d}\lambda,k\in\mathrm N^*$
    • 任意相邻两个条纹之间的距离 $\Delta x=\frac{D}{d}\lambda$ 。
• 劈尖干涉
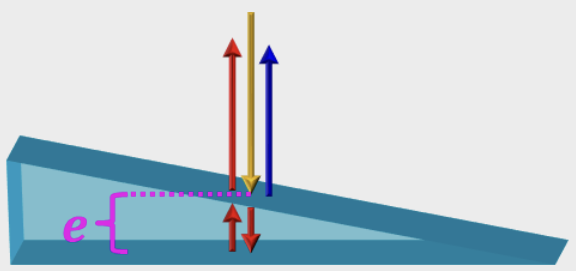
  • 原理图
    • 
  • 光程差分布
    • 在劈的厚度为 $e$ 的位置，上下表面两束光的光程差为 $\delta=2ne+\delta'$，$\delta'$ 为额外光程差。
    • $\delta'$ 取决于两束光是否有半波损失，如果都有或都没有，则取 $0$，否则取 $\frac{\lambda}{2}$。
    • 亮纹： $\delta=k\lambda,k\in \mathrm N^*$
    • 暗纹： $\delta=\frac{2k-1}{2}\lambda,k\in \mathrm N^*$
    • 对于尖端处，$e=0$，如果 $\delta'=0$，则为亮纹，如果 $\delta'=\frac{\lambda}{2}$，则为暗纹。
  • 位置分布
    • 相邻两个条纹之间的距离 $L=\frac{\Delta e}{\sin\theta}=\frac{\lambda}{2n\sin\theta}$。
    • $L$ 与条纹的级数无关。
• 牛顿环
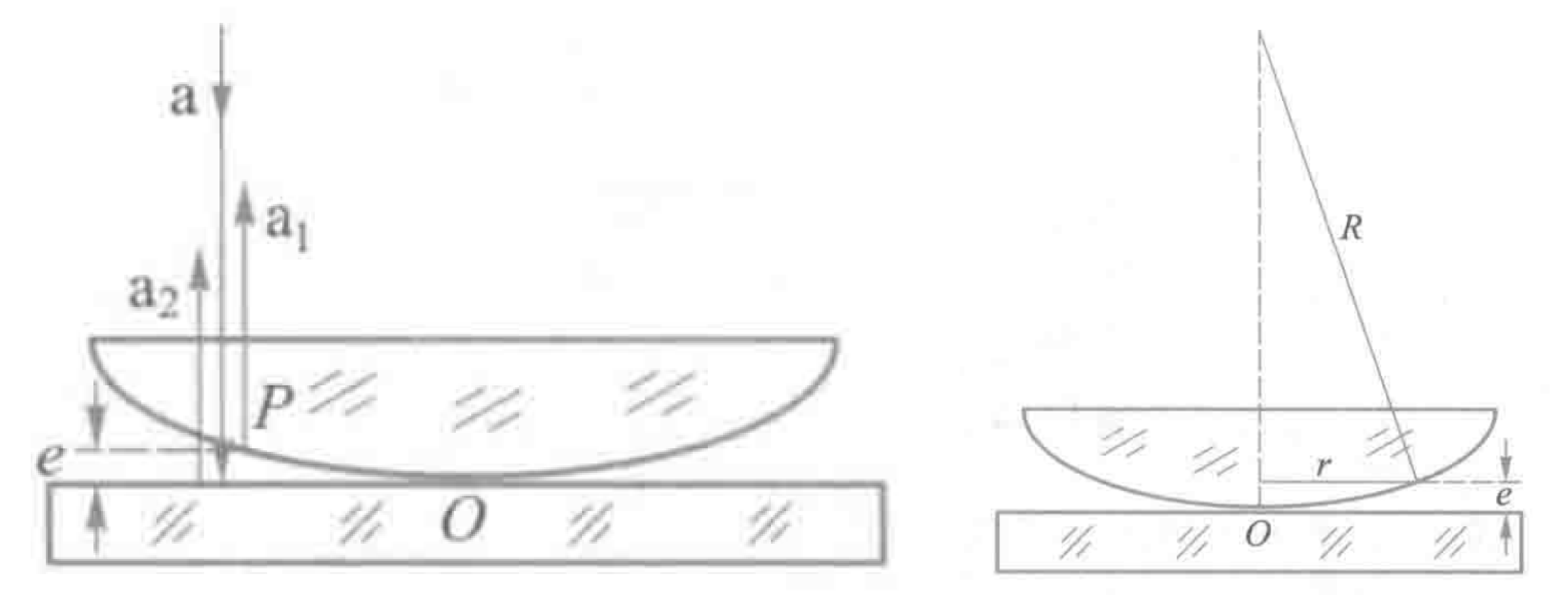
  • 原理图
    • 
  • 位置分布
    • 设 $R$ 为平凸透镜的曲率半径，$r$ 为曲面某处距中心轴的距离，$e$ 为此处空气部分的厚度。
    • 根据原理图可以得到 $r^2=R^2-(R-e)^2=2Re-e^2\approx 2Re\implies e=\frac{r^2}{2R}$
    • 光程差的关系与劈尖干涉一致，结合可以得出位置分布。