组合功能模块
- 基本逻辑函数
- 1 位函数
- 当只有 位变量 时,函数 只有 种情况:。
- 用 接地表示, 用 接 或 表示。
- 时,在 和 之间接非门。
- 多位函数
- 输入变量 有 个位时,可以表示用向量 表示,特定分量用 表示。
- 1 位函数
- 使能
- 使能控制输入信号传递到输出端是否被屏蔽,被屏蔽时输出保持为一个非使能值。
- 使用与门实现使能:, 时 ,否则 。
- 使用或门实现使能:, 时 ,否则 。
- 译码器
- 定义
- 译码器将一种 位二进制编码转换为一种 位的输出码,输出码最多只有一位为 。
- 输入为 位、输出为 位的译码器称为 - 译码器。
- 译码器可以带有使能功能,当 时有译码结果,否则没有。
- 简单译码器
- 1-2 译码器有 位输入 ,有 位输出 。
- ,。
- 2-4 译码器有 位输入 ,有 位输出 。
- ,,,。
- 1-2 译码器有 位输入 ,有 位输出 。
- 分级组合译码器
- 一个 - 的译码器可以由 - 译码器和 - 译码器组成,。
- 将 位二进制输入 拆分为 位的高位部分 和 位的低位部分,分别接入两个译码器。
- 最终每个输出 为两个译码器对应部分的输出 和 接与门。
- 不考虑两个译码器内的逻辑门,最终需要 个与门。
- 一个 - 的译码器使用一个 输入的译码器和一个 输入的译码器,门输入成本最低。
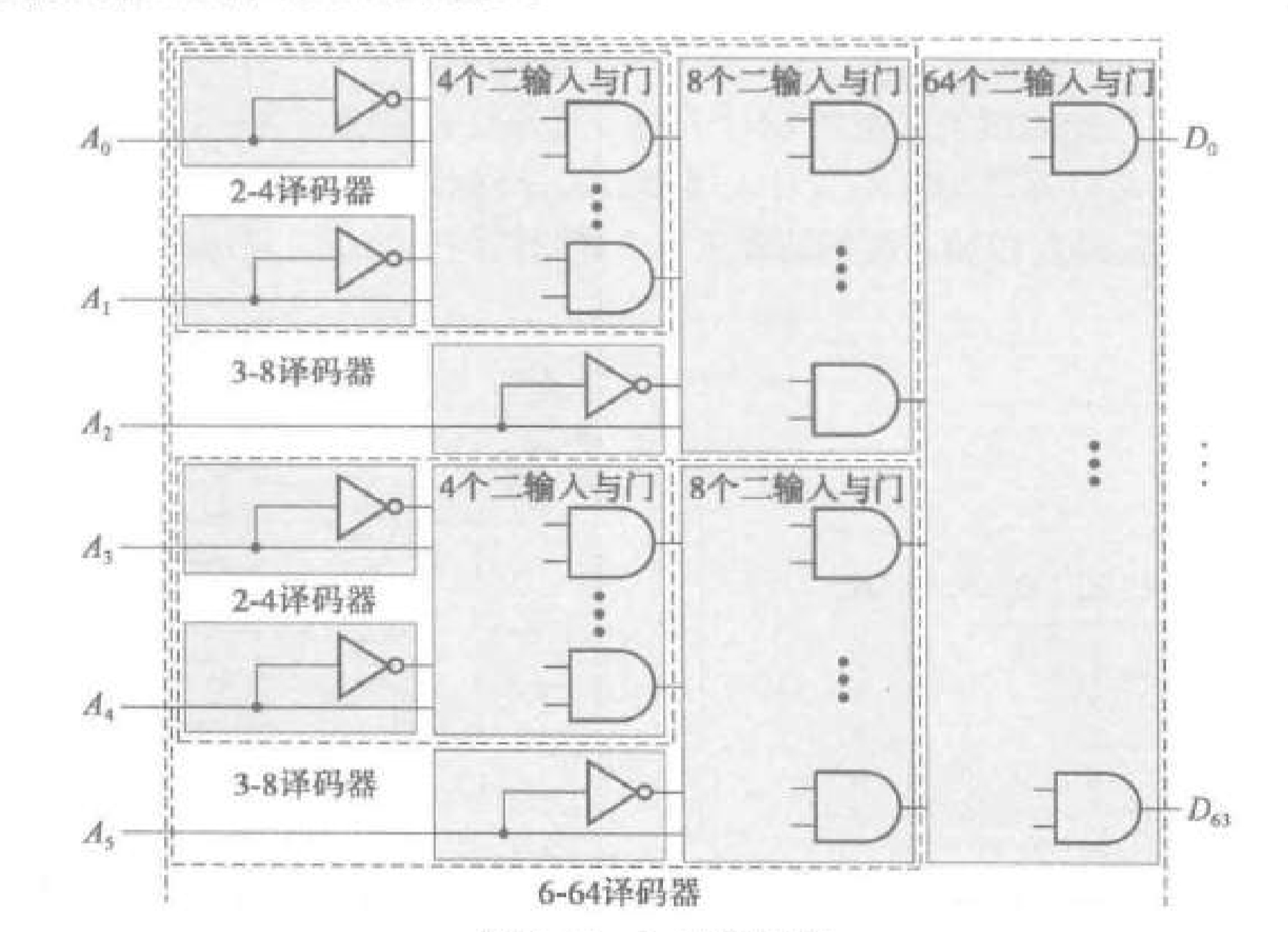
- 一个 - 的译码器可以由 - 译码器和 - 译码器组成,。
- 译码器和布尔函数
- 变量布尔函数 有 个最小项,分别对应 - 译码器的各个输出。
- 将 取值为 的最小项对应的译码器输出用或门连接,则或门输出为 。
- 定义
- 编码器
- 定义
- 编码器是译码器的逆过程。
- 个输入、 个输出的编码器记作 - 编码器。输入记作 ,输出记作 。
- 普通编码器
- 普通的 - 编码器假设 个输入中任何时刻都有且仅有一个位为 。
- 输出使用或门连接输入,若某输入为 时当前输出应为 ,则或门要连接这个输入。
- 如果普通编码器有多个输入为 ,则最终输出结果是每个 输入单独出现时的结果取或。
- 优先编码器
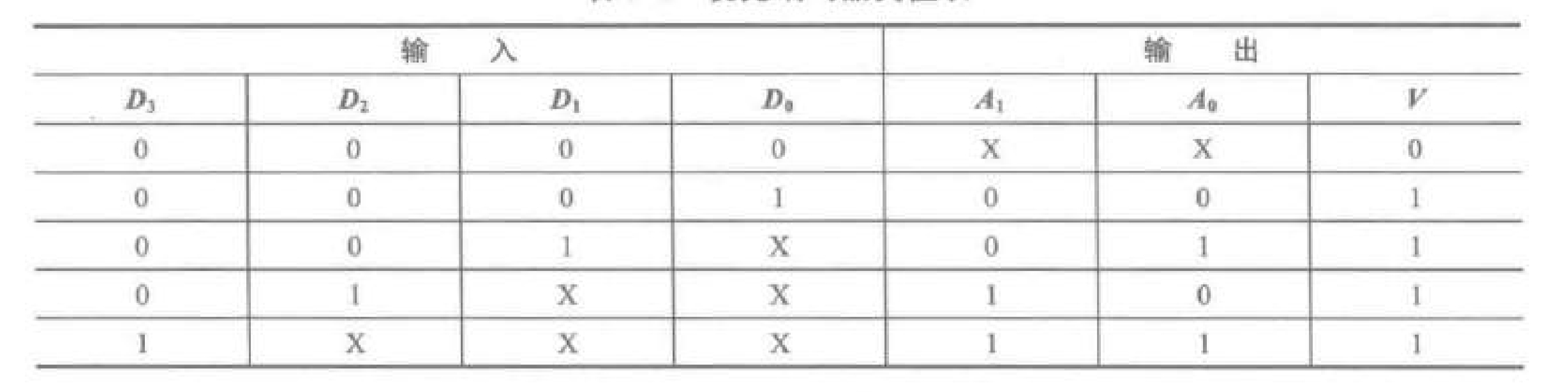
- 优先编码器定义了输入的优先级(一般是高位优先级高),多个输入为 时编码高优先级输入。
- 优先编码器除了编码输出,还有 输出,表示是否有值输入,用所有输入的或实现。
- 高位优先级高时,真值表可以改为紧凑真值表。
- 有 行,全 输入时,。
- 时,,,,表示取值任意。
- 定义
- 多路复用器
- 定义
- - 多路复用器从 个输入中选择一个,用 个选择输入控制。
- 表示复用一条线路输出。
- - 多路复用器的实现:
- 由一个 - 译码器、 个与门、一个 输入或门组成。
- 译码器输入接控制输入 。
- 第 个与门接译码器输出 和输入 。
- 输入或门的输入接所有与门,输出为 。
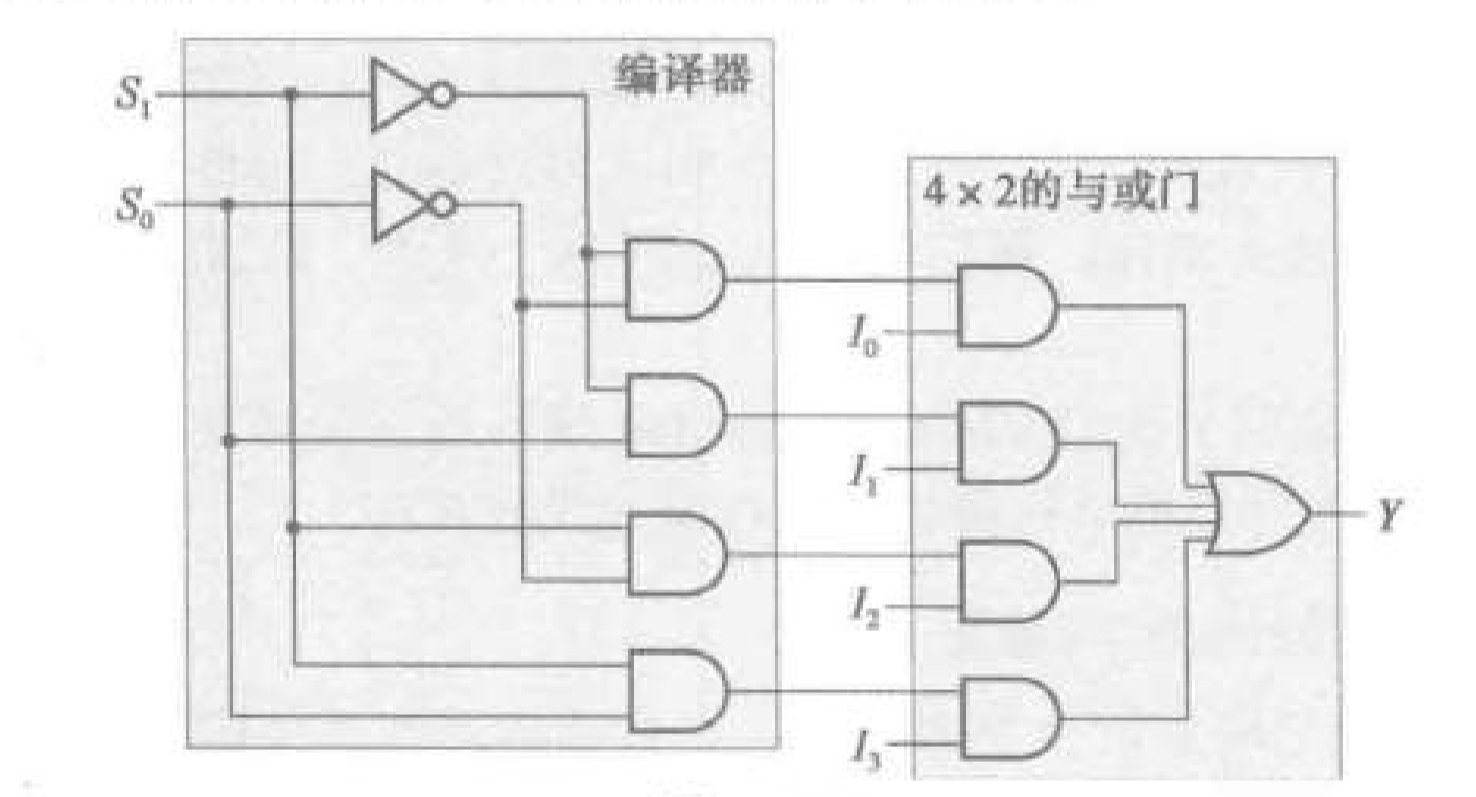
- - 多路复用器从 个输入中选择一个,用 个选择输入控制。
- 多重多路复用器
- 重 - 多路复用器从 个 位输入中选择一个。
- 重 - 多路复用器的实现:
- 由一个 - 译码器、 个与门、 个 输入或门组成。
- 第 个 输入或门接 个与门,这些与门中,第 个输入接 和 。
- 第 个 输入或门输出为 。
- 多路复用器与布尔函数
- 给定一个 变量布尔函数 ,用 - 多路复用器的实现方法:
- 每个最小项 对应多路复用器输入 。
- 若 ,则 连接 ,否则连接 。
- 用 - 多路复用器的实现方法:
- 仅考虑前 个变量组成的最小项 ,对应多路复用器输入 。
- 对于 ,前 个变量取值已经固定, 退化为最后一个变量的函数。
- 根据真值表中 和 最小项的取值,接 。
- 如果用 - 多路复用器的实现,则 可能接的布尔函数有 种。
- 给定一个 变量布尔函数 ,用 - 多路复用器的实现方法:
- 定义
- 加法器
- 半加器
- 半加器输入两个加数 ,输出和 和进位 。
- ,。
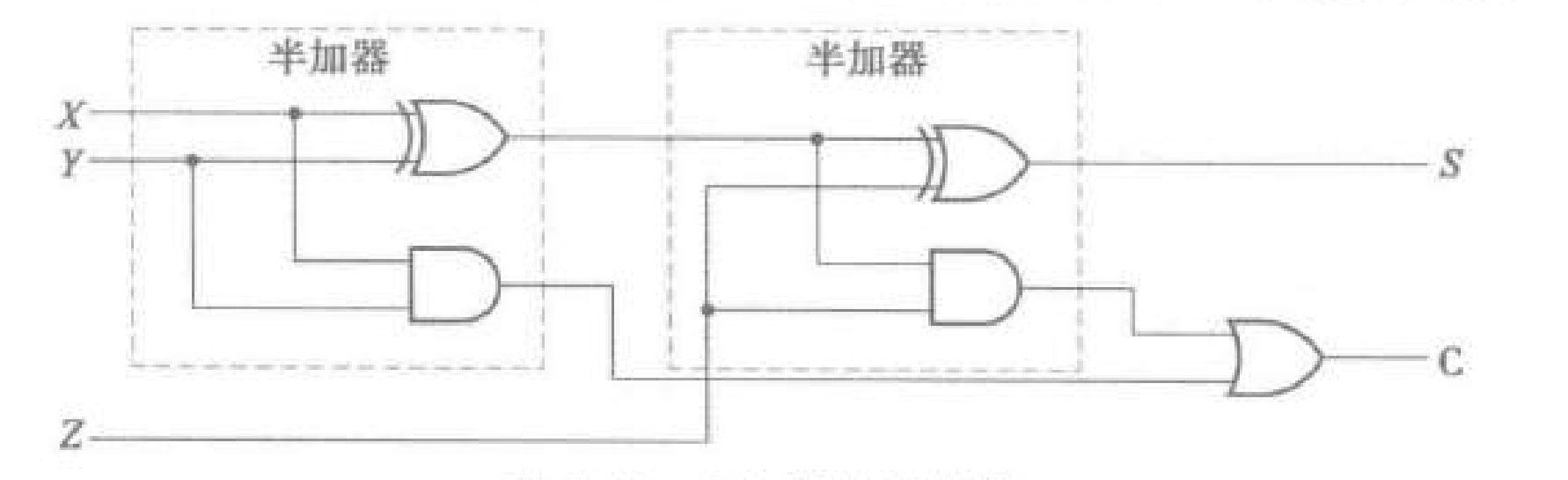
- 全加器
- 全加器输入两个加数 和低位进位 ,输出和 和进位 。
- 。
- 。
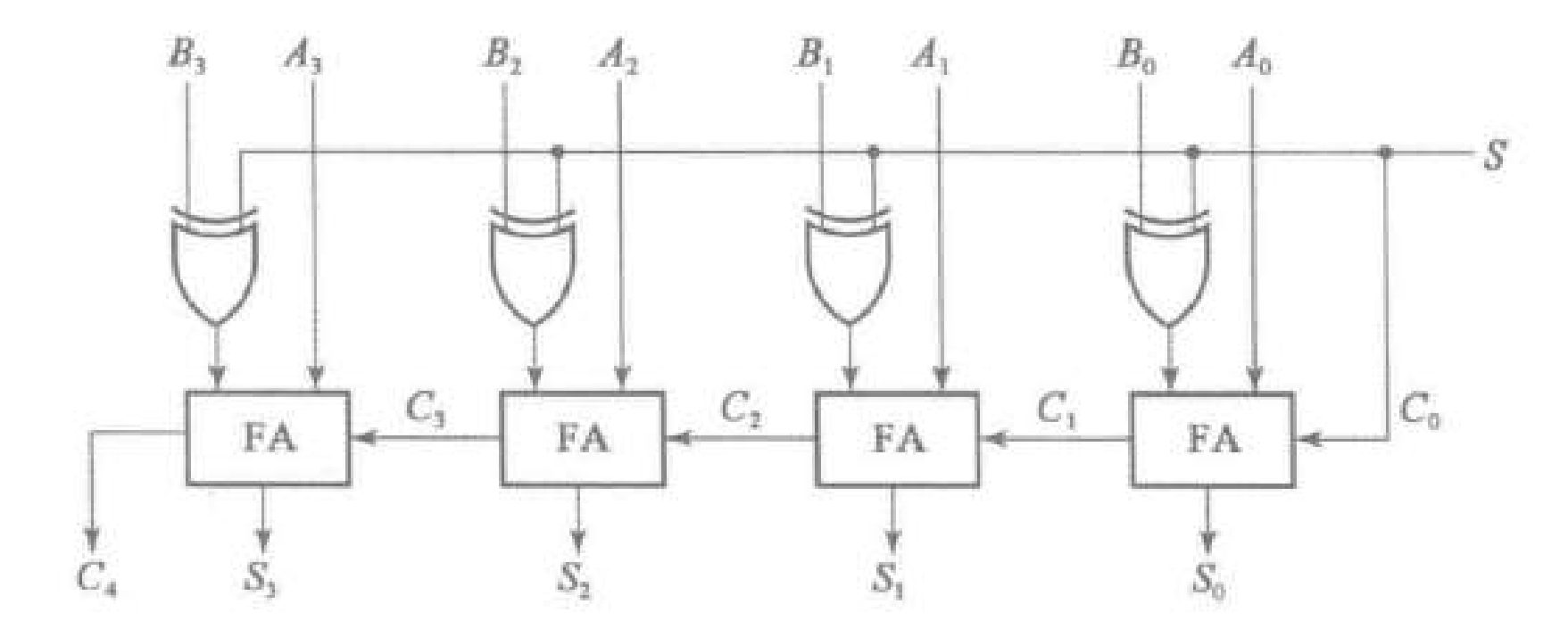
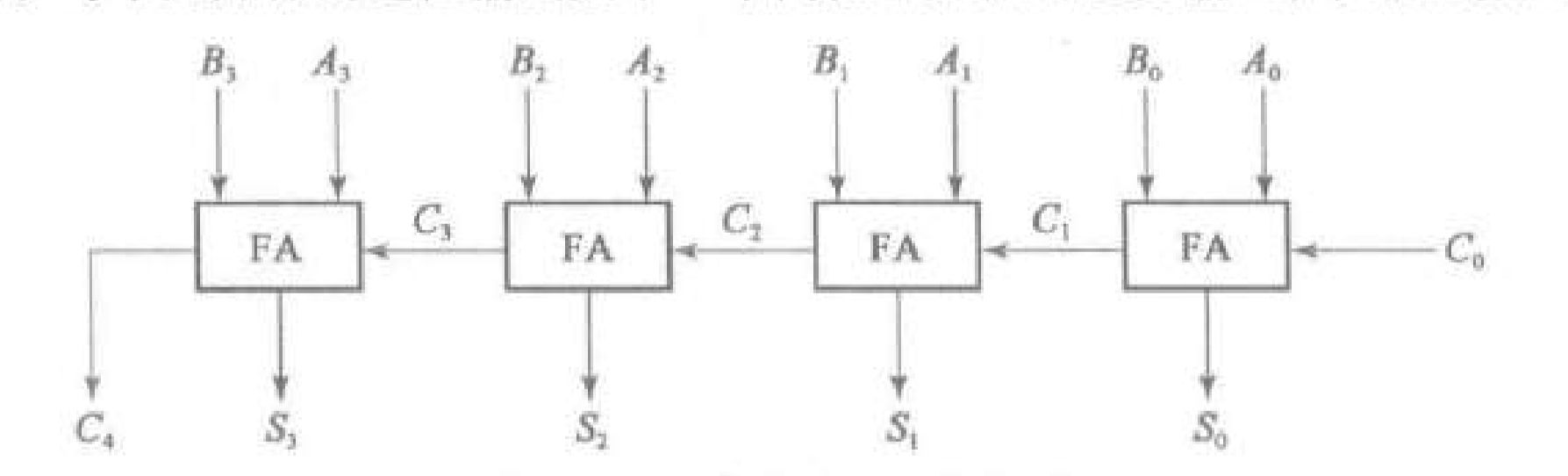
- 行波加法器
- 位行波加法器由 个全加器组合而成,输入为两个加数 ,最低位进位 ,输出和 。
- 定义第 个全加器的中间进位为 。
- 第 个加法器的低位进位输入接 。
- 半加器
- 减法器
- 递增器
- 使用加法器实现:
- 令 。
- 令 。
- 使用加法器实现:
- 递减器
- 使用加法器实现:令 。
- 常数乘法器
- 位常数乘法器中设 为常数, 为输入。
- 当 时,结果为 左移 位。
- 实现只需要令 ,其他位为 。
- 对于任意的 ,结果为所有 。
- 实现时使用加法器累加每一个项,若 则跳过,否则将 左移 位再累加。
- 常数除法器
- 位常数除法器中设 为输入, 为输出。
- 此处仅考虑 ,结果为 右移 位。